Design.
Business analysis.
Business boundaries.
The system only contains the remaining ticket management portion of the ticket.That is, query the remaining seats, order tickets to reduce seats.
Generating order information, payment, traffic control, request wind control, etc. are not included in the scope of this discussion.
Business use cases.
- Check the remaining tickets to find out the number of trips available between the two stations and the number of seats remaining.
- Query the ticket ticket stake corresponding to the number of trains, can query the given number of trains, between the stations there are how many remaining seats.
- Seat selection is supported, and customers can select a given number of train and seats and place an order to buy a ticket.
Difficulty analysis
Ticketing management.
The difficulty of the management of train tickets for the rest of the ticket is in fact the peculiarity of the inventory of the remaining tickets.
The common e-commerce commodity, with SKUs as the smallest unit, is independent of each other and not affected by each other.
Train tickets are different because the remaining tickets will be affected by the start and end of the sold tickets.Here's a simple logical model to take a detailed look at this particularity.
Now, let's assume that there is a number of cars passing through four stations, a, b, c, d, and at the same time, we simplify the scenario, assuming that there is only one seat in the train.
So before anyone buys a ticket, the remaining tickets for this ride are as follows:
| Stations | The amount of remaining tickets. |
|---|---|
| a,b | 1 |
| a, c | 1 |
| a, d | 1 |
| b,c | 1 |
| b,d | 1 |
| c, d | 1 |
If a customer now has purchased a,c ticket.So since there is only one seat, there are no tickets other than c,d.The rest of the ticket situation becomes the following:
| Stations | The amount of remaining tickets. |
|---|---|
| a,b | 0 |
| a, c | 0 |
| a, d | 0 |
| b,c | 0 |
| b,d | 0 |
| c, d | 1 |
To put it more bluntly, if a customer buys a, d, all remaining tickets will become 0.Because the passenger was always sitting in the seat.
This is the special nature of the train ticket: the same seat of the same train, the number of remaining tickets at each end point will be affected by the starting point of the ticket sold.
What`s more, it's easy to conclude that there is no such effect between different seats in the same car.
Remaining ticket inquiries.
As mentioned in the previous section, due to the particularity of the remaining ticket inventory.For the same train a, b, c, d, there are 6 possible ticket options.
And it's easy to conclude that the number of types selected is actually calculated by selecting a combination of 2 in the n sites, which is c (n, 2).
So if there is a car passing through 34 stations, the possible combination is c (34,2) s 561.
How to efficiently respond to multiple queries that may exist is also something that the system needs to address.
Claptrap Main Design
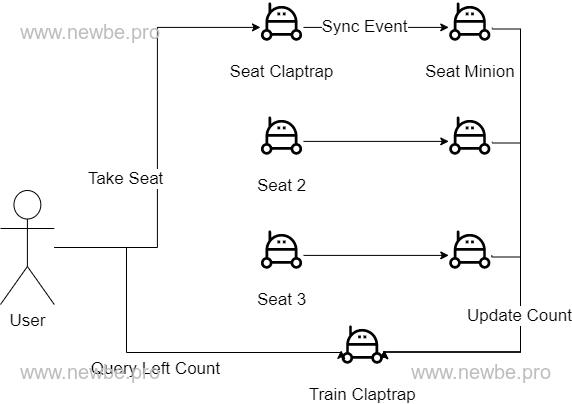
Each seat on the same train is designed as a Claptrap - SeatGrain.
The State of the Claptrap contains a basic information.
| Type | Name | Description |
|---|---|---|
| IList<int> | Stations | A list of the id of the Pathways Station, starting with the Origin Station, ending with the Terminal.Verification at the time of primary ticket purchase. |
| Dictionary<int, int> | StationDic | The index reverse dictionary that routes the station id.Stations are a list of index-ids, and the dictionary is the corresponding id-index dictionary, in order to speed up queries. |
| List<string> | RequestIds | Key properties.On each interval, the purchased ticket id.For example, an index of 0 represents a ticket id from station 0 to station 1.If it is empty, there is no subscription ticket. |
With the design of this data structure, two businesses can be implemented.
Verify that it can be purchased
By passing in two station ids, you can find out if this belongs to this SeatGrain.And query all the interval segments corresponding to the start and end points.Just judge whether all segments in the RequestIds do not have a ticket ID.If not, it can be purchased.If there is already a ticket purchase ID on any section, the purchase is no longer possible.
For example, the current situation with Stations is 10, 11, 12, 13. RequestIds, on the other, are 0,1,0.
So, if you're buying a 10->12 ticket, that's not possible because the second range of RequestIds has already been purchased.
However, if you want to>10- 11 tickets, you can, because no one in the first range of RequestIds has yet to buy them.
Buy
Just place the starting and ending points on all the interval segment settings in RequestIds.
Design the remaining ticket for all seats on the same ride as a Claptrap-TrainGran
The Claptrap State contains some basic information
| Type | Name | Description |
|---|---|---|
| IReadOnlyList<int> | Stations | A list of the id of the Pathways Station, starting with the Origin Station, ending with the Terminal.Verify while query. |
| IDictionary<StationTuple, int> | SeatCount | Key properties.The StationTuple represents a start to the end.The collection contains the rest of the ticket situation for all possible starting points.For example, according to the above, if the car passes through 34 locations, the dictionary contains 561 key-value pairs |
Based on the data structure above, you only need to synchronize the corresponding information to the Grain each time The SeatGrain completes placing the order.
For example, if a,c has a ticket purchase, the remaining tickets for a,c/a,b/b,c will be reduced by one.
This can be achieved with the Minion mechanism built into this framework.
It is worth mentioning that this is a bigger design than the "minimum competitive resource".Because the query scenario does not need to be absolutely fast in that business scenario.This design reduces the complexity of the system.