The Newbe.Claptrap framework is ideal for solving business systems with complicity problems.The train ticketing system is a very typical scenario use case.
In this series, we'll step through the business, code, testing, and deployment aspects of how to use the Newbe.Claptrap framework to build a simple train ticketing system.
Bragging first hits the draft
Let's first define the business boundaries and performance requirements required for this simple train ticketing system.
Business boundaries.
The system only contains the remaining ticket management portion of the ticket.That is, query the remaining seats, order tickets to reduce seats.
Generating order information, payment, traffic control, request wind control, etc. are not included in the scope of this discussion.
Business use cases.
- Check the remaining tickets to find out the number of trips available between the two stations and the number of seats remaining.
- Query the ticket ticket stake corresponding to the number of trains, can query the given number of trains, between the stations there are how many remaining seats.
- Seat selection is supported, and customers can select a given number of train and seats and place an order to buy a ticket.
Performance requirements
- The average cost of querying the remaining tickets and ordering must not exceed 20ms.This time only includes service-side processing time, i.e. page network transmission, page rendering, and so on are not parts of the framework's concern.
- Residual ticket queries can have a delay, but not more than 5 seconds.Delay means that there may be a query for tickets, but no tickets are allowed to be ordered.
Difficult analysis
Ticketing management.
The difficulty of the management of train tickets for the rest of the ticket is in fact the peculiarity of the inventory of the remaining tickets.
The common e-commerce commodity, with SKUs as the smallest unit, is independent of each other and not affected by each other.
For:I'm currently selling 10,000 Armstrong roundabouts from the planet Sebotan, red and white, respectively.Then when the user under orders, as long as the control of red and white two items of inventory is not oversold.There is no relationship between them.
However, the remaining tickets for the train are different, as the remaining tickets will be affected by the end of the tickets sold.Here's a simple logical model to take a detailed look at this particularity.
Now, let's assume that there is a number of cars passing through four stations, a, b, c, d, and at the same time, we simplify the scenario, assuming that there is only one seat in the train.
So before anyone buys a ticket, the remaining tickets for this ride are as follows:
| Stations | The amount of remaining tickets. |
|---|---|
| a,b | 1 |
| a, c | 1 |
| a, d | 1 |
| b,c | 1 |
| b,d | 1 |
| c, d | 1 |
If a customer now has purchased a,c ticket.So since there is only one seat, there is no other ticket except c,d.The rest of the ticket situation becomes the following:
| Stations | The amount of remaining tickets. |
|---|---|
| a,b | 0 |
| a, c | 0 |
| a, d | 0 |
| b,c | 0 |
| b,d | 0 |
| c, d | 1 |
To put it more bluntly, if a customer buys a, d, all remaining tickets will become 0.Because the passenger was always sitting in the seat.
This is the special nature of the train ticket: the same seat of the same train, the number of remaining tickets at each end point will be affected by the starting point of the ticket sold.
What`s more, it's easy to conclude that there is no such effect between different seats in the same car.
Remaining ticket inquiries.
As mentioned in the previous section, due to the particularity of the remaining ticket inventory.For the same train a, b, c, d, there are 6 possible ticket options.
And it's easy to conclude that the number of types selected is actually calculated by selecting a combination of 2 in the n sites, which is c (n, 2).
So if there is a car passing through 34 stations, the possible combination is c (34,2) s 561.
How to efficiently respond to multiple queries that may exist is also something that the system needs to address.
Claptrap logical design
Actor mode is a design pattern that is inherently suitable for solving problems with problems with problems.The Newbe.Claptrap framework based on this concept can naturally handle the difficulties mentioned above.
Minimum competitive resources
Compared with the concept of "resource competition" in multithreaded programming, the author puts forward the concept of "minimum competitive resource" in the business system.With this concept, it's easy to find design points for how to apply Newbe.Claptrap.
For example, in the author's example of selling Abstrom gyration cannons, each item in the same color is a "minimum competitive resource".
Note that this is not to say that all items under the same color are a "minimum competitive resource".Because, if 10,000 goods are numbered, then the rush to buy goods 1 and goods 2, there is no competition.Therefore, each commodity is a Minimal Competing Resources.
So in the case of train tickets, the smallest competitive resource:the same seat on the same train.
As mentioned above, the same seat on the same train, in the selection of different starting and ending points is that the remaining ticket situation there is a competitive relationship.Specifically, for example, the author wants to buy tickets for a,c, while readers want to buy tickets for a,b.Then we have a competitive relationship, and we will only have one person who can successfully purchase this "minimum competitive resource".
Here are some examples that the author thinks are available:
- In a business system that allows only single-ended logins, a user's login ticket is the Minimal Competing Resources.
- In a configuration system, each configuration item is the Minimal Competing Resources.
- In a stock market, each buy or sell order is Minimal Competing Resources.
This is the author's own assumptions, no reference to other materials, if there is similar information or nouns can support the content, but also hope that readers can leave a message description.
Minimum competitive resources with Claptrap
"Minimum competitive resources" are mentioned because distinguishing between the least competitive resources is an important basis for system design when designing Claptrap's State.
Here's a conclusion::Claptrap's State should be at least greater than or equal to the "minimum competitive resource."
Combined with the example of the Absterrand swing acceleration gun, if all items of the same color are designed in the same Claptrap State (larger than the minimum competitive resource).Well, different users buy goods to influence each other, because, the Actor pattern based on the Claptrap is the queuing processing request.That is to say, assuming that each item needs to process 10ms, it also takes 10000* 10 ms to process all the purchase requests as soon as you want.But if each item is numbered, each item is designed as a separate Claptrap State.Well, since they are not related to each other.Selling all the goods would theoretically only cost 10ms.
That:if Claptrap's State is larger than the minimum competitive resource range, the system will not have a problem with correctness, but there may be some performance losses.
Further, as mentioned earlier in the example of train ticketing, the same seat on the same train is the least competitive resource, so we can design this business entity as Claptrap's State.But what if the design range is smaller than this?
For:we designed Claptrap's State as a residual ticket for the same seat on the same train at different departure points.Then, there is a very traditional question of:"How to ensure the correctness of data in a distributed system".For this point, the author can not expand, because the author also can not say clearly, just hasty drop a conclusion:"If Claptrap's State is less than the scope of the smallest competitive resources, the relationship between Claptrap will become difficult to deal with, there are risks."
Claptrap Main Design
Next, combine the theories described above.We threw out the design directly.
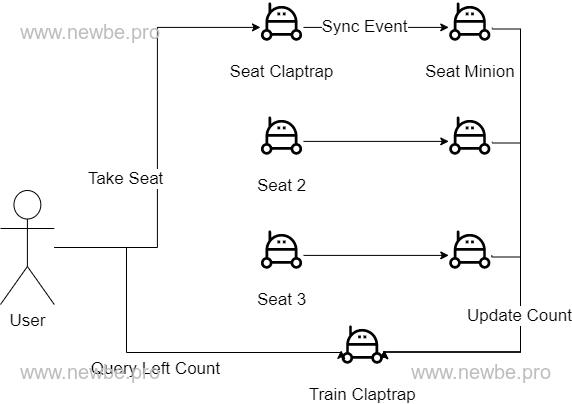
Each seat on the same train is designed as a Claptrap - SeatGrain.
The State of the Claptrap contains a basic information.
| Type | Name | Description |
|---|---|---|
| IList<int> | Stations | A list of the id of the Pathways Station, starting with the Origin Station, ending with the Terminal.Verification at the time of primary ticket purchase. |
| Dictionary<int, int> | StationDic | The index reverse dictionary that routes the station id.Stations are a list of index-ids, and the dictionary is the corresponding id-index dictionary, in order to speed up queries. |
| List<string> | RequestIds | Key properties.On each interval, the purchased ticket id.For example, an index of 0 represents a ticket id from station 0 to station 1.If it is empty, there is no subscription ticket. |
With the design of this data structure, two businesses can be implemented.
Verify that it can be purchased
By passing in two station ids, you can find out if this belongs to this SeatGrain.And query all the interval segments corresponding to the start and end points.Just judge whether all segments in the RequestIds do not have a ticket ID.If not, it can be purchased.If there is already a ticket purchase ID on any section, the purchase is no longer possible.
For example, the current situation with Stations is 10, 11, 12, 13. RequestIds, on the other, are 0,1,0.
So, if you're buying a 10->12 ticket, that's not possible because the second range of RequestIds has already been purchased.
However, if you want to>10- 11 tickets, you can, because no one in the first range of RequestIds has yet to buy them.
Buy
Just place the starting and ending points on all the interval segment settings in RequestIds.
Unit test cases
The following links allow you to view the code implementation of the above algorithm:
Design the remaining ticket for all seats on the same ride as a Claptrap-TrainGran
The Claptrap State contains some basic information
| Type | Name | Description |
|---|---|---|
| IReadOnlyList<int> | Stations | A list of the id of the Pathways Station, starting with the Origin Station, ending with the Terminal.Verify while query. |
| IDictionary<StationTuple, int> | SeatCount | Key properties.The StationTuple represents a start to the end.The collection contains the rest of the ticket situation for all possible starting points.For example, according to the above, if the car passes through 34 locations, the dictionary contains 561 key-value pairs |
Based on the data structure above, you only need to synchronize the corresponding information to the Grain each time The SeatGrain completes placing the order.
For example, if a,c has a ticket purchase, the remaining tickets for a,c/a,b/b,c will be reduced by one.
This can be achieved with the Minion mechanism built into this framework.
It is worth mentioning that this is a bigger design than the "minimum competitive resource".Because the query scenario does not need to be absolutely fast in that business scenario.This design reduces the complexity of the system.
Summary
In this article, through business analysis, we have come up with a combination of train ticket residual management and Newbe.Claptrap.
We'll then focus on the design of this article, explaining how to develop, test, and deploy.
In fact, the project source code has been built, and readers can get the:
Special thankswangjunjx8868interface created with Blazor for this example.