设计
业务分析
业务边界
该系统仅包含车票的余票管理部分。即查询剩余座位,下单买票减座。
而生成订单信息,付款,流量控制,请求风控等等都不包含在本次讨论的范围中。
业务用例
- 查询余票,能够查询两个车站间可用的车次以及剩余座位数量。
- 查询车次对应的车票余票,能够查询给定的车次,在各个车站之间还有多少剩余座位。
- 支持选座下单,客户能够选择给定的车次及座位,并下单买票。
实现难点分析
余票管理
火车票余票管理的难点,其实就在于其余票库存的特殊性。
普通的电商商品,以 SKU 为最小单位,每个 SKU 之间相互独立,互不影响。
火车票余票,却有所不同,因为余票会受到已卖票起终点而受到影响。下面结合一个简单的逻辑模型,来详细的了解一下这种特殊性。
现在,我们假设存在一个车次,分别经过 a,b,c,d 四个站点,同时,我们简化场景,假设车次中只有一个座位。
那么在没有任何人购票之前,这个车次的余票情况就如下所示:
| 起终点 | 余票量 |
|---|---|
| a,b | 1 |
| a,c | 1 |
| a,d | 1 |
| b,c | 1 |
| b,d | 1 |
| c,d | 1 |
如果现在有一位客户购买了一张 a,c 的车票。那么由于只有一个座位,所以除了 c,d 之外的余票也就都没有。余票情况就变成了如下所示:
| 起终点 | 余票量 |
|---|---|
| a,b | 0 |
| a,c | 0 |
| a,d | 0 |
| b,c | 0 |
| b,d | 0 |
| c,d | 1 |
更直白一点,如果有一位客户购买了全程车票 a,d,那么所有的余票都将全部变为 0。因为这个座位上始终都坐着这位乘客。
这也就是火车票的特殊性:同一个车次的同一个座位,其各个起终点的余票数量,会受到已售出的车票的起终点的影响。
延伸一点,很容易得出,同一车次的不同座位之间是没有这种影响的。
余票查询
正如上一节所述,由于余票库存的特殊性。对于同一个车次 a,b,c,d,其可能的购票选择就有 6 种。
并且我们很容易就得出,选择的种类数的计算方法实际上就是在 n 个站点中选取 2 个的组合数,即 c(n,2) 。
那么如果有一辆经过 34 个站点的车次,其可能的组合就是 c(34,2) = 561 。
如何高效应对可能存在的多种查询也是该系统需要解决的问题。
Claptrap 主体设计
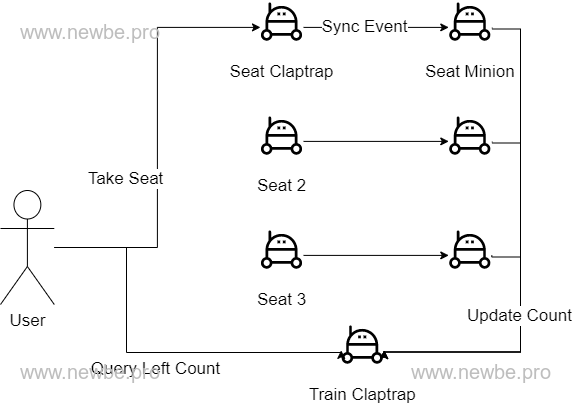
将同一车次上的每个座位都设计为一个 Claptrap - SeatGrain
该 Claptrap 的 State 包含有一个基本信息
| 类型 | 名称 | 说明 |
|---|---|---|
| IList<int> | Stations | 途径车站的 id 列表,开头为始发站,结尾为终点站。主要购票时进行验证。 |
| Dictionary<int, int> | StationDic | 途径车站 id 的索引反向字典。Stations 是 index-id 的列表,而该字典是对应的 id-index 的字典,为了加快查询。 |
| List<string> | RequestIds | 关键属性。每个区间上,已购票的购票 id。例如,index 为 0 ,即表示车站 0 到车站 1 的购票 id。如果为空则表示暂无认购票。 |
有了这数据结构的设计,那么就可以来实现两个业务了。
验证是否可以购买
通过传入两个车站 id,可以查询到这个作为是否属于这个 SeatGrain 。并且查询到起终点对应的所有区间段。只要判断这个从 RequestIds 中判断是否所有的区间段都没有购票 Id 即可。若都没有,则说明可以购买。如果有任何一段上已有购票 Id,则说明已经无法购买了。
举例来说,当前 Stations 的情况是 10,11,12,13. 而 RequestIds 是 0,1,0。
那么,如果要购买 10->12 的车票,则不行,因为 RequestIds 第二个区间已经被购买。
但是,如果要购买 10->11 的车票,则可以,因为 RequestIds 第一个区间还无人购买。
购买
将起终点对应在 RequestIds 中所有的区间段设置上购票 Id 即可。
将同一车次上的所有座位的余票情况设计为一个 Claptrap - TrainGran
该 Claptrap 的 State 包含有一些基本信息
| 类型 | 名称 | 说明 |
|---|---|---|
| IReadOnlyList<int> | Stations | 途径车站的 id 列表,开头为始发站,结尾为终点站。主查询时进行验证。 |
| IDictionary<StationTuple, int> | SeatCount | 关键属性。StationTuple 表示一个起终点。集合包含了所有可能的起终点的余票情况。例如,根据上文,如果该车次经过 34 个地点,则该字典包含有 561 个键值对 |
基于以上的数据结构,只需要在每次 SeatGrain 完成下单后,将对应的信息同步到该 Grain 即可。
例如,假如 a,c 发生了一次购票,则将 a,c / a,b / b,c 的余票都减一即可。
这里可以借助本框架内置的 Minion 机制来实现。
值得一提的是,这是一个比“最小竞争资源”大的设计。因为查询场景在该业务场景中不需要绝对的快速。这样设计可以减少系统的复杂度。